3D Reconstruction
- Enrique Shinohara
- 18 abr 2022
- 3 Min. de lectura
For the second assignment, we were asked to write from scratch, a program to simulate stereo images reconstruction. For this, we will describe the whole process followed during this assignment. Firstly it is convenient as usual to split the problem into blocks to later solve the bigger picture, so, we have the following structure:
Feature extraction
Correspondance between features
Triangulation

To start, we need to prepare the environment and understand it, for this, we were given. We can accomplish this by drawing points in the 3D scene along with the image captured by each camera. It is important to note that the coordinates X, Y, and Z correspond to the vectors (point (0,0,0) in the scene) of colours R, G, and B respectively.
Now that we have a better understanding of the values with the coordinates in the scene and the image, we move on to the implementation of the stereo image reconstruction algorithm.
Feature extraction
Feature extraction is done as advised in the assignment, for the computational difficulty of the problem. The most interesting feature in a simple reconstruction problem will be the edges of the object we are trying to reconstruct, so to do this, a Canny Edge Detection Algorithm is pretty reliable and easy to use.
We can extract features by using Canny as we can see in the previous left image, but because this gives us unnecessary features that add complexity to the computation, a Gaussian Blur encourages obtaining fewer feature points without losing the main structure of the scene to reconstruct.
Correspondance between features
For the correspondence between features, we decided to implement a Sum of Squared Differences. But before we do this, we have to "simplify" the job of the matcher which can be done thanks to the epipolar restriction.
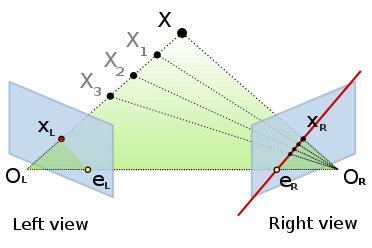
As we can observe in the previous image, the epipolar restriction gives us an epipolar line in which we will always find the point from the opposite image that we are looking for.
To get this epipolar line, we use HAL.graficToOptical() to convert a 2D point from the left image to the 3D reference system coordinates and backproject it with HAL.backproject(). By getting two points along this projection line, we can then project it again with HAL.project() but this time onto the right image plane. The line crossing these two projected points will be our epipolar line.
This greatly reduces the searching time, because we only have to look along the line and not the whole image.
Template Matching
Now that we have the line where we can find the right correspondence point of the left image feature, we need to implement an algorithm to know if the point from the right image is the same point selected from the left image. For this, we will use the Sum of Squared Differences (SSD) to analyze the similarity between two patches, the patch with the greatest SSD will be the position of our left feature in the right image.
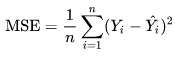
Very similar to the Mean Squared Error, without the mean, and a size of 47 for the window search, it is possible to always obtain the correct correspondence between the two images.
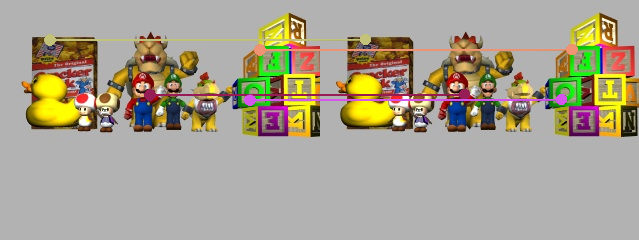
Triangulation
Finally, once we have the features correspondence of the left and right image, we need to triangulate both points to obtain the reconstructed point onto the 3D scene. The triangulation process consists in using the retro-projection of both the left and right cameras from which we will obtain the 3D point by searching for the crossing point of the two retro-projection lines.
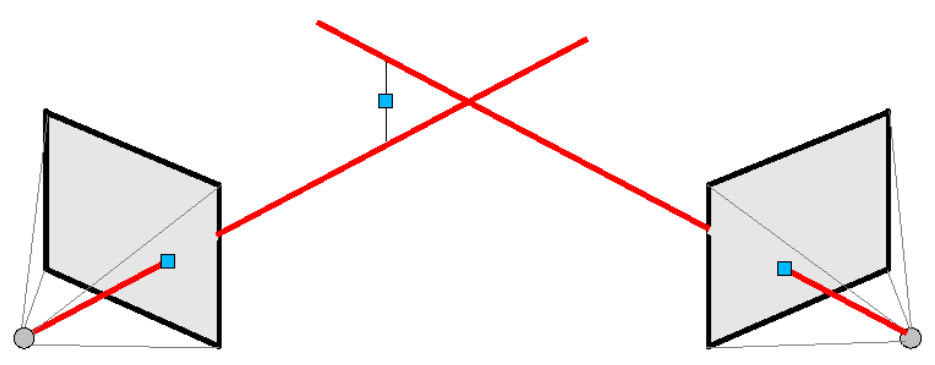
For the previous idea to work, we would require a perfect calibration of the camera and a perfect correspondence between the position of the left feature and the right, but it is really difficult to set this almost "perfect" configuration, this is why the two retro-projected lines would never cross in one single point. To find a workaround to this problem, the idea is instead of searching for the crossing point, we search for the shortest line between the two 3D lines. For this, we have used a documented implementation of the algorithm by Paul Bourke.
Results and conclusion
Finally, the results obtained from the reconstruction are as follows. The overall picture of the scene is visible as well as the depth of each object. The algorithm itself is pretty good, obtaining the coordinates of each point in 4-5 minutes and without assuming a canonical configuration of the cameras, this means that the epipolar line is being computed for each point making it robust for other possible configurations.









Comentarios